2021-05-27 11:03
前回、機械学習の開発環境を整える方法を解説し、 Windows上に、Visual Studio Code(VS Code), Anaconda, PyTorchをインストールしました。
前回の記事:Pytorchで機械学習1:Anaconda/VS Codeで環境構築編
今回はニューロ(機械学習)の基礎を簡単に解説し、PyTorchのプログラムで動かす方法を示します。 シンプルな例として、2入力1出力のXOR問題というものを学習するプログラムを解説します。
ニューロの構成
ニューロの計算は実際の神経細胞の仕組みを模擬しています。 神経細胞を模擬すれば、生物を模倣できるのでは?という発想です。
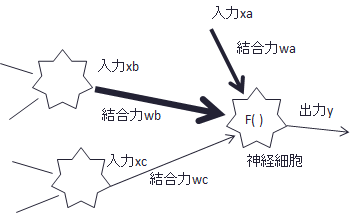
神経細胞を簡単に模式化すると下図のようになります。
各神経細胞は相互に結合しており、複数のニューロンからシグナルを入力し、その合計を関数f()に通してシグナルが出力されるという仕組みです。 また、それぞれの入力には結合力があり、重みがかけられます(図では線の太さで表現)。
数式で表すと下記のようになります。biasはオフセット量です。
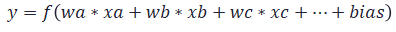
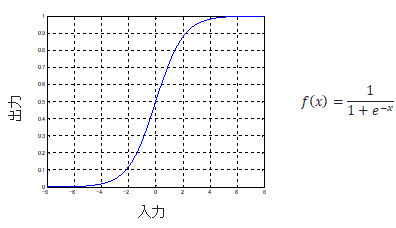
関数f()は、昔は下記のようなシグモイド関数が一般的でした。 入力が小さいとほぼ出力せず、ある入力レベルを超えると出力し始める、という神経細胞の動きを真似ています。
(最近はReLU関数及びその改良版が主流で、これにより深い層のDeep Learningが可能になったといわれます。)
とにもかくにも、ニューロは基本的にシグモイド関数などの非線形関数の合成近似と言えます。 非線形関数近似の方法は他にも(フーリエ変換のように三角関数の合成など)考えられると思いますが、とりあえずこのような方法で上手くいっているということだと思います。
今回使用する階層型ニューロの構成
機械学習で使用されるニューロの構成として、階層型ニューロがよく使用されます。 階層型ニューロの構成は、下図のように、入力層,中間層、出力層により構成されます。 任意に中間層を増やしたり、各層のニューロン(神経細胞)を増やすこともできます。
(今回の説明では煩雑になるのでバイアス項の説明は省略します。簡単に言うと、入力値が1のユニットを裏で追加すると、バイアスの更新も重みの更新と同様に推論/学習させることができます。)
ここでは説明を簡単にするため、
- 入力層のニューロン:2個
- 中間層のニューロン:2個
- 出力層のニューロン:1個
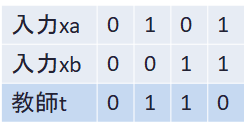
具体的に学習させるデータを決めましょう。今回は入力(xa,xb)に対する教師(t)を下表のように定めます。例えば、(xa,xb)=(0,0)のときt=0を出力。論理演算のXORを学習させます。
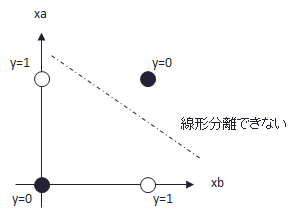
これを学習させて何が面白いのかと言うと、下図のように、1本の線でグループを分類できないため、線形分離不可能な問題となるためです。即ち、非線形問題となるのです。 そのため、XOR問題は非線形問題を解けるか判断するためのファーストステップとして用いられることがあります。
ニューロの学習
ニューロの学習方法について解説します。
先に示した演算の出力結果yと教師tの関係から、それらの損失関数(評価関数)を定め、これを最小とするような、重みwを求めていきます。
損失関数は色々なものがありますが、今回は下記のモノを使います。
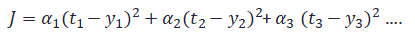
tとyが一致していたら、0となる、というものです。
αは重みです。重要なものには重みを大きくします。また、例えば、速度と位置と次元の異なるものを評価する場合も重みづけが必要となります。
解くべき最適化問題は「Jを最小化するような重みwを求めること」となりました。
最急降下法を用いて解く場合、重みの更新は次のようにあらわすことができます。wを少し変化させたときの損失関数Jの変化量と、逆符号にちょっとだけ更新するという意味になります。 偏微分になっているのは、Jは複数のwの関数ですが、そのうち一つの変数について微分するためです。
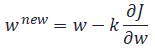
具体的に解き方を示します。まず今回の例の評価関数を下記のように定義します。
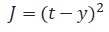
また、シグモイド関数の微分は計算すると下記のように表すことができます。
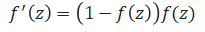
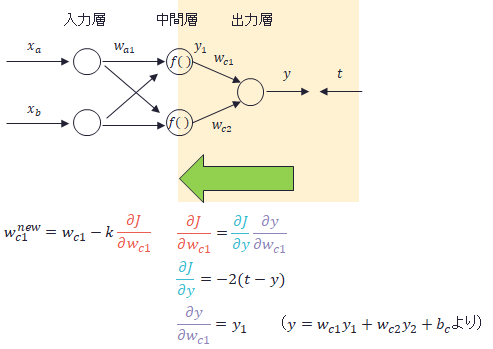
2層目と3層目の間の重みの更新は下記のようになります。最初の赤文字の偏微分の内容を展開していくと、全て既知の値となることがわかります。
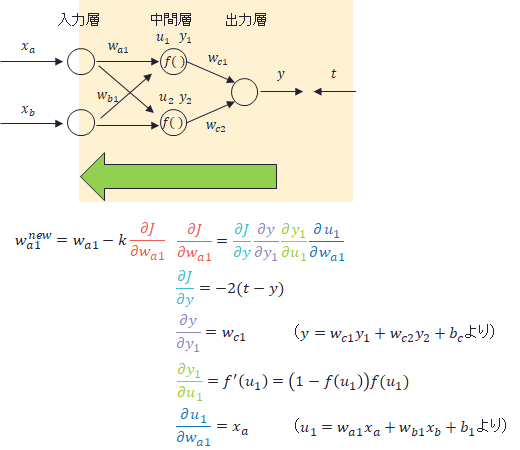
同様に1層目と2層目の間の重みの更新は下記のようになります。
以上のように、学習時は最終段から逆方向に演算が進んでいくので、誤差逆伝播法(Back Propagation, BP法)と呼ばれます。
このアルゴリズムの弱点は現在の値付近の偏微分で計算しているので、ローカルミニマムに陥る可能性があるところです。 それを解決するために確率的勾配降下法などが用いられますが、それでも限界はあるということは心に留めておくと良いでしょう。
以上、学習のアルゴリズムとして、誤差逆伝播法について解説しました。実はPyTorchを使うとこの内容を直接書く必要はなく、自動的に処理されるのですが、一度は自分で計算してみると良いでしょう。
PyTorchによるxor問題を解くプログラム
いよいよPyTorchでのプログラム例を示します。
全ソースはページ末尾にまとめています。
まず最初に入力xと教師tの設定です。
PyTorchを使用するにはtorch.tensorという型にしなければなりません。 Python配列やnumpyとtorch.tensorの相互変換が可能です。 ここでは配列をtorch.tensor型にしています。
# input x, teacher t x = torch.tensor([[1,1],[1,0],[0,1],[0,0]], dtype=torch.float32) t = torch.tensor([[0],[1],[1],[0]], dtype=torch.float32)
次に、TensorDataset、DataLoaderについて解説します。
まず、TensorDatasetを使って、xとtのデータセット(dataset)を作成します。
ところで、ニューロの学習は1セットずつ流すよりも、複数セットを流してそれぞれの更新量を合計(or平均)して、まとめて更新するのが一般的ですが、 このまとめて更新することをミニバッチと呼んでいます。
DataLoaderを使用することで、datasetの中から、ミニバッチの組の順番をシャフルして出力することができます。 戻り値のtrain_loaderの内部で状態を持っているので、train_loaderにアクセスするごとに適切にデータがシャッフルされて出力ます(今回の例では4セット分ランダムな並び)。
一般的にGPUを用いて演算する場合、ミニバッチのサイズはGPUのメモリサイズで制限が来るので、エラーにならない範囲で大きくするのが良いと思います。
# dataset dataset = TensorDataset(x,t) # data loader train = dataset batch_size = 4 # mini batch size train_loader = DataLoader(train, batch_size, shuffle=True)
次にいよいよニューロ本体の定義です。nn.Moduleクラスを継承してNetというクラスをつくります。
__init__()関数はコンストラクタです。 ここで全結合関数のfc1とfc2を定義します。
forward()関数はnn.Moduleから継承された関数で、ここに順伝播の処理を書きます。 入力層2,中間層2,出力層1ユニットのニューロ演算が定義できているのが分かると思います。 fc1,fc2の定義と実行がpython独特な書き方なので多少戸惑いますが、慣れれば分かりやすいと思います。
# My Neural Network
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
mid = 2 # mid layer
# input:2 mid:2
self.fc1 = nn.Linear(2,mid)
# mid:2 output:1
self.fc2 = nn.Linear(mid,1)
def forward(self, x):
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
return x
# new
net = Net()
損失関数の定義。MSELossは二乗誤差の関数。reductionで平均とするか、和にするかを選択できます。(他にはnn.CrossEntropyLossがよく使われます)
criterion = nn.MSELoss(reduction="sum")
最適化法の定義。SGDは確立的再急降下法。lrは学習係数で発散しない程度に大きい値にします。
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
そして学習の実行です。
外側のforはmax_epoch+1回分(ここでは2001回)実行されます
内側のforは一度だけ実行されます。即ち、train_loaderで4パターンが一度にランダムで出力され、4パターン分を一度に処理します。
内側のforの内部の処理は大体上記ソースように書くようになります。
optimizser.zero_grad() は微分情報をクリアするものです。今はとりあえず必要と思っていてください。
y=net(x)で、forward関数が実行されます。
loss.backward()は誤差逆伝播の演算です。どこにも誤差逆伝播の面倒な処理を書いていませんが、torch.tensorの自動微分の機能で自動的に演算されています。これがPyTorchの凄いところです。
なお、よくみると、netとlossのoptimizserの関係がややこしくみえますが(私の感覚だとloss.backward()でなくnet.backward(), optimizser.step()でなくnet.step()としたくなる)、こういうものと覚えておきましょう。
実行中に誤差loss.item()が表示するようにしました(.item()はtorch.tensor型の1変数を出力)。この誤差が0に近づけば良いということになります。
# Train
print("+++TRAIN+++")
max_epoch=2000
for epoch in range(max_epoch+1) :
for batch in train_loader:
x,t = batch
#clear grad
optimizer.zero_grad()
#forward
y=net(x)
#loss function
loss = criterion(y,t)
#BP
loss.backward()
#update
optimizer.step()
if epoch % 500 == 0:
print("epoc:", epoch, ' loss:', loss.item())
実行結果は、下記のようにlossがほぼ0に収束すれば正常に学習されたと言えます。
+++TRAIN+++ epoc: 0 loss: 9.5293607711792 epoc: 500 loss: 0.9907403588294983 epoc: 1000 loss: 0.07182814180850983 epoc: 1500 loss: 3.693934047532821e-10 epoc: 2000 loss: 4.508393658397836e-12
そして推論です。正しく学習されたか確認しましょう。
ここで注意が必要で、推論では学習を行わないので、事前にnet.eval()、torch.no_grad()という処理が必要です。推論では学習しないので微分演算が不要(あると処理に無駄な時間がかかる)なのでそれを止めるために入れます。 定型処理といえるでしょう。
あとはxを入力してyが出力され、表示しています。この場合はyが0に近ければ正解です。
# Test
print("+++Test+++")
net.eval()
with torch.no_grad() :
x = torch.tensor([0.0, 0.0])
y = net(x)
print(x,y)
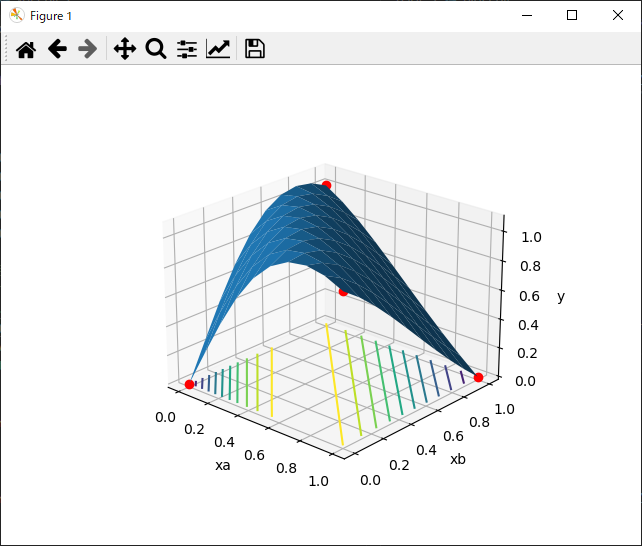
最後に、3Dのグラフで解の分布を描画するコードを入れています。 xa, xbは0か1が入る想定で学習しましたが、中間の値を含めて(例えば、xa=0.3, xb=0.7)、全ての値をプロットし、解を結んで曲面に表したものです。
また赤い丸は実際に学習させた(xa,xb,t)=(0,0,0),(0,1,1),(1,0,1),(1,1,0)での点です。
このグラフから次のことが分かります。
- 曲面で入出力関係の分布を学習することが出来たので、非線形問題も解けるということを目でみて納得できます。
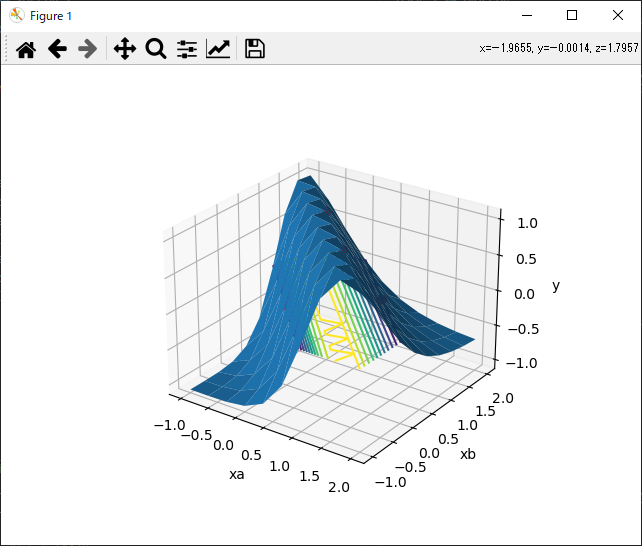
- 一つ下の図のように、レンジを広げてプロットすると、シグモイド関数を立体的に合成したものということが分かると思います。 中間層が2個なので、シグモイド関数2個分というのも見て取れると思います。
- ニューロは学習したもの以外でも推論ができる(汎化能力)と言われますが、確かにグラフをみると多少赤丸からズレた場所でもそれらしく推論できることが分かります。 汎化能力というと生命の神秘的な響きがありますが、シグモイド関数等で近似しているので当然といえば当然です。 また、もう少し汎化能力を上げたい場合は周辺も学習させたほうが良いだろうなどと思いつきます。
Deep Learningへ
今回解説したニューロのアルゴリズム自体は数十年前からあるものです。
Deep Learningはこれからどう進化したかと言うと、その名の通り、深い層の学習が出来るようになったのが特徴的です。
即ち、今回解説したニューロでは3層としましたが、より深い(多い)層の場合は、学習が中々進みません。理由はシグモイド関数を使用しているからです。 誤差逆伝播の計算にシグモイド関数の微分を使いますが、中央付近以外は値が小さく(0.1等)、段数が増えるとそれが累積されて(0.1 * 0.1 * 0.1 = 0.001倍..等)殆ど重みの更新がされない、という問題があったためです。
深層化できない問題に対応するために、シグモイド関数を別の関数、例えばReLU等に変更することで深層化できるようになってきました。
さらに画像処理等ではCNN(畳み込みニューラルネットワーク)と呼ばれるものが発展し、何段にも連なる深いネットワークの学習を可能にしています。
演習
(大学の教科書みたいに解答は無いです。スイマセン)
- 演習1:torch.manual_seed(123)で乱数シードを設定していますが、これをその他の値にしたときにどうなるか試してみよう。
- 演習2:for batch in train_loader:の内側で、xやtのサイズを確認してみましょう。(print(x.shape)等)
- 演習3:同様に、batch_size = 4を1や2や10などにした場合、xやtのサイズや、ループ回数がどうなるか確認しよう。
- 演習4:nn.MSELoss(reduction="sum")をnn.MSELoss()にすると学習スピードが落ちます。何故でしょうか。ヒント
- 演習5:torch.optim.SGD(net.parameters(), lr=0.1)の、lrを大きくしたり、小さくしたりして、学習速度や発散するかをみてみましょう。
まとめ
XOR問題を題材に、ニューロのプログラムをPyTorchで解説しました。
XOR問題の良いところは、モデルが単純なため、グラフ化して理解しやすいためです。2入力1出力以内でないと、もうグラフ化するのが困難で、 中身が良く分からなくなってきます。
XOR問題は原理的に、今回のモデルのように、中間層1層でそのユニット数は2個で学習が完了するはずですが、収束しない場合も結構でてきます。 何故だろうと、調べていると原理的なことが段々とみえてくると思います。
ブログにまとめるためにサラッと学習できたように書いていますが、xor問題は意外と非線形性が強くローカルミニマムに陥り易く、学習させるのに苦労します。
全ソース
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
# Random initialization
torch.manual_seed(123)
# input x, teacher t
x = torch.tensor([[1,1],[1,0],[0,1],[0,0]], dtype=torch.float32)
t = torch.tensor([[0],[1],[1],[0]], dtype=torch.float32)
print("x=",x)
print("t=",t)
# dataset
dataset = TensorDataset(x,t)
# data loader
train = dataset
batch_size = 4 # mini batch size
train_loader = DataLoader(train, batch_size, shuffle=True)
# My Neural Network
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
mid = 2 # mid layer
# input:2 mid:2
self.fc1 = nn.Linear(2,mid)
# mid:2 output:1
self.fc2 = nn.Linear(mid,1)
def forward(self, x):
x = self.fc1(x)
x = torch.sigmoid(x)
x = self.fc2(x)
return x
# new
net = Net()
print("Initial weights")
print(net.fc1.weight.data)
print(net.fc1.bias.data)
print(net.fc2.weight.data)
print(net.fc2.bias.data)
# Loss function
criterion = nn.MSELoss(reduction="sum")
# Stochastic gradient descent
optimizer = torch.optim.SGD(net.parameters(), lr=0.1)
# Train
print("+++TRAIN+++")
max_epoch=2000
for epoch in range(max_epoch+1) :
for batch in train_loader:
x,t = batch
#clear grad
optimizer.zero_grad()
#forward
y=net(x)
#loss function
loss = criterion(y,t)
#BP
loss.backward()
#update
optimizer.step()
if epoch % 500 == 0:
print("epoc:", epoch, ' loss:', loss.item())
print("Final weights")
print(net.fc1.weight.data)
print(net.fc1.bias.data)
print(net.fc2.weight.data)
print(net.fc2.bias.data)
# Test
print("+++Test+++")
net.eval()
with torch.no_grad() :
x = torch.tensor([0.0, 0.0])
y = net(x)
print(x,y)
x = torch.tensor([1.0, 0.0])
y = net(x)
print(x,y)
x = torch.tensor([0.0, 1.0])
y = net(x)
print(x,y)
x = torch.tensor([1.0, 1.0])
y = net(x)
print(x,y)
# +++3D Graph+++
# x=0~1, xb=0~1
xa_np = np.linspace(0, 1, 10)
xb_np = np.linspace(0, 1, 10)
xa_np, xb_np = np.meshgrid(xb_np, xa_np) # make grid
# 2D array -> 1D array
xa_np1d = np.ravel(xa_np)
xb_np1d = np.ravel(xb_np)
# Combine two 1D arrays
x = np.stack([xa_np1d, xb_np1d], 1)
# Convert to torch type
x = torch.from_numpy(x.astype(np.float32)).clone()
# run test
y = net(x)
# Convert to np type
y_np = y.to('cpu').detach().numpy().copy()
# Convert to 10x10 array
y_np = y_np.reshape(10, 10)
# Draw 3D graph
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(xa_np, xb_np, y_np)
ax.plot(0,0,0,'or') # (xa,xb,t)
ax.plot(0,1,1,'or')
ax.plot(1,0,1,'or')
ax.plot(1,1,0,'or')
ax.set_xlabel('xa')
ax.set_ylabel('xb')
ax.set_zlabel('y')
ax.contour(xa_np, xb_np, y_np,offset = -0.001,
levels=np.linspace(0, 1, 11)) # level is 0.1 step
plt.show()